A matemática é uma das disciplinas onde os alunos têm mais dificuldades. Entre fórmulas, funções, equações, cálculos e exercícios matemáticos, há muito por onde se perder e a resposta dada pelo professor nem sempre é a mais indicada. Mas conhecer cada fórmula, função e equação é essencial para avançar nas aulas de matematica e ser capaz de resolver os exercícios. Em particular, é importante dominar a função afim, saber se é constante, decrescente ou crescente, e como representar cada coeficiente. Mas sabe sequer o que é uma função afim?
A função afim é um conceito fundamental na álgebra e na matemática aplicada. No estudo das funções, a função afim é uma das mais simples e fáceis de compreender, porque estabelece uma correspondência direta e proporcional entre duas grandezas. A sua forma mais básica é a de uma linha reta no plano cartesiano, mas é necessário dominar essa fórmula para ser capaz de compreender funções mais complexas no futuro. Para o ajudar, criamos este artigo com as informações essenciais sobre as funções afim e como as calcular!

Função afim: definição e teorema
A função afim é uma função de primeiro grau, que representa uma relação de proporcionalidade entre as variáveis independentes e dependentes, com um possível deslocamento linear. Uma função afim pode ser definida pela fórmula: f (x)= ax + b.
onde:
- a é o coeficiente angular, que define a inclinação da reta no gráfico;
- b é o coeficiente linear, que indica o ponto onde a reta intercepta o eixo y quando x = 0.
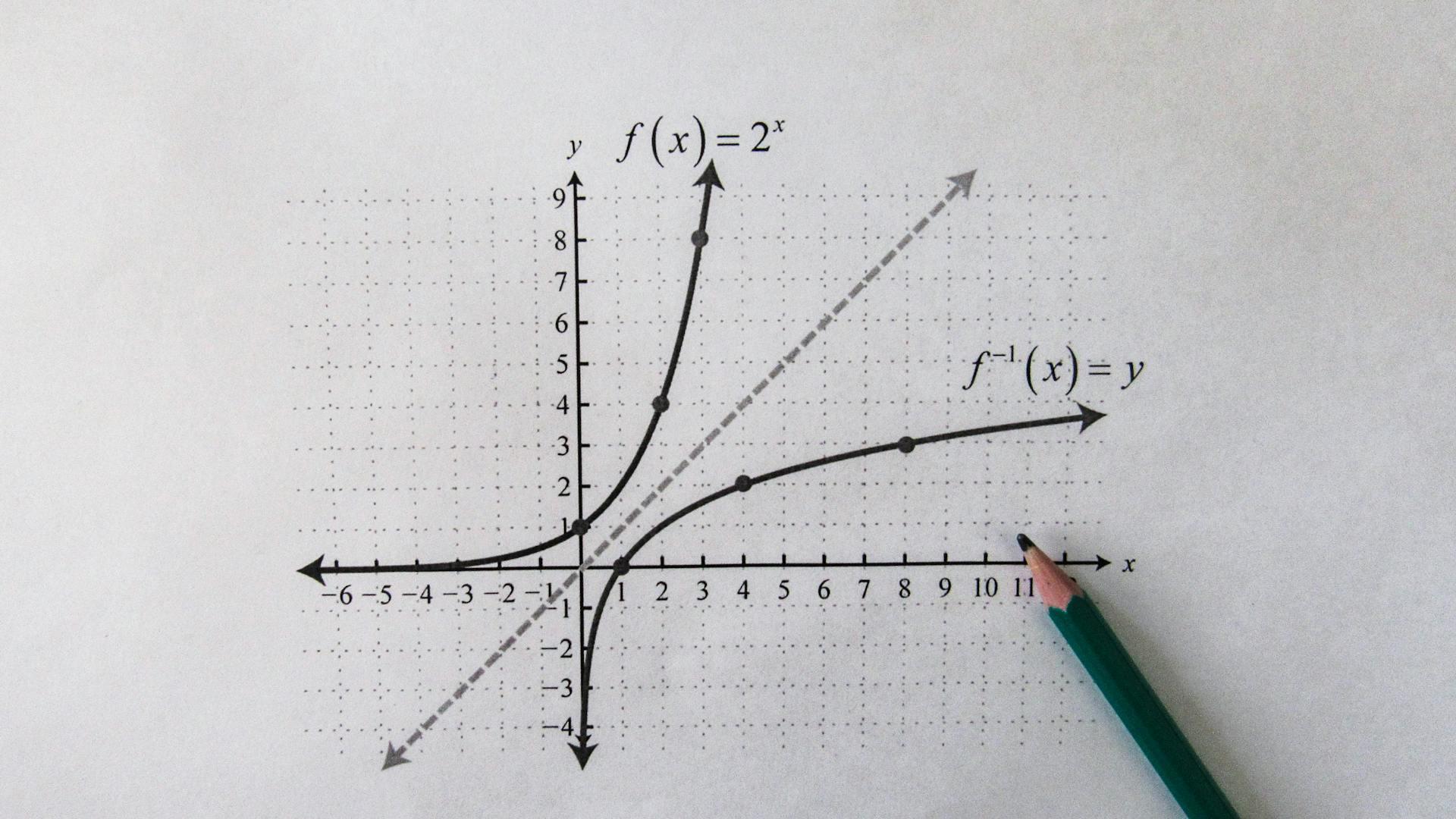
Ou seja, a função afim apresenta uma relação direta entre a variável independente x e a variável dependente y, de forma a que para cada valor de x existe um valor correspondente de y, formando uma linha reta no plano cartesiano. Este modelo linear é a base de muitas aplicações matemáticas que lidam com mudanças proporcionais, devido à simplicidade com que se ajusta a dados que seguem uma tendência linear.
Os elementos de uma função afim são essenciais para entender como se comporta e como podemos interpretá-la graficamente.
- Coeficiente angular (a): este coeficiente determina a inclinação da reta. Se a for positivo (a>0), a função é crescente, o que indica que o valor de y aumenta com x. Se for negativo (a<0), a função é decrescente, ou seja, y diminui conforme x aumenta. Quando a=0, a função torna-se uma reta horizontal, representando uma função constante. Assim, o coeficiente angular indica a taxa de variação de y em relação a x;
- Coeficiente linear (b): representa o valor de y quando x=0, ou seja, é o ponto onde a reta intercepta o eixo vertical. Este valor define o deslocamento da reta no plano cartesiano, e é crucial para definir a posição da função sem alterar sua inclinação;
É essencial que seja capaz de distinguir entre o coeficiente angular e o coeficiente linear, se quer fazer a representação gráfica corretamente.
Estes dois coeficientes fornecem todas as informações necessárias para determinar a função afim e a sua posição no plano cartesiano, facilitando a interpretação gráfica. Mas como é que representa graficamente?
Veja como ter explicações matemática online.
A representação gráfica de uma função afim
Representar a função afim no plano cartesiano envolve traçar a reta que passa por pelo menos dois pontos. O ponto de intercetação com o eixo y é dado por b, enquanto a inclinação é determinada pelo coeficiente a. Em alguns casos, podemos também escolher dois valores distintos para x, calcular os valores correspondentes para y utilizando a fórmula da função, e então traçar a reta.
Para exemplificar, consideremos a função f (x) = 3x + 2:
- O valor de b = 2 indica que a reta cruza o eixo y no ponto (0, 2);
- O valor de a = 3 mostra que para cada unidade de x, y aumenta em três unidades.
Para desenhar o gráfico de uma função afim, deve seguir os seguintes passos:
- Definir o ponto de intercetação com o eixo y: este ponto é dado diretamente pelo valor de b. Como f (0) = b, o ponto (0,b) será o ponto onde a reta cruza o eixo y;
- Determinar a inclinação da reta usando o coeficiente angular a: a partir do ponto de intercetação com o eixo y, o valor de a indica quantas unidades a reta sobe ou desce para cada unidade que avançamos em x. Por isso, se a = 2, por exemplo, ao movermos uma unidade para a direita, a reta sobe duas unidades.
Com essas informações, é possível determinar o comportamento da função afim e traçar a sua representação gráfica com precisão.
Aulas com explicações matematica Lisboa.
Como determinar uma função afim?
Determinar uma função f é fácil se conhecermos os valores de a e b. Vejamos um exemplo concreto f (x) = 2x - 3. Neste caso, f (2) = 1, f (-2) = -7 e f (1) = -1.
Se quisermos tentar determinar esta função afim, podemos utilizar dois métodos distintos: leitura no eixo de coordenadas e cálculo.
Determinar uma função afim a partir da representação gráfica
É o método mais simples, e aquele pelo qual os alunos de matemática começam a aprender.

Mas à medida que vai avançado nas aulas, é provável que o professor de matemática lhe peça para resolver os exercícios sem ter acesso aos gráficos.
Para determinar graficamente f (x) = 2x - 3, basta ver quais são os pontos da reta que intercetam os eixos x e y.
No nosso caso, encontramos os pontos A (0; -3), B (2; 1) e C (3;3), dos quais deduzimos que a reta d1 apresenta uma equação do tipo y = 2x - 3.
Determinar uma função afim através de cálculos
Se não tiver acesso à representação gráfica ou o professor de matemática pedir para utilizar cálculos para obter a função afim, existe uma fórmula indicada a utilizar. Vejamos como!
Quando f é uma função afim não linear, os valores de x em f (x) não são proporcionais. No entanto, podem ser encontrados entre os valores de x. Ou seja:
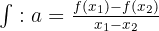
Para calcular o coeficiente de direção com dois números x1 e x2 e sua representação f : a, temos x1 = 0y x2 = 0, com f (x1) = -3 e f (x2) = 1.
Aplicações das funções afim
As funções afins são extremamente versáteis e aparecem em diversas áreas práticas. Em economia, por exemplo, podem ser utilizadas para modelar o custo de produção de um item com base numa taxa fixa e um custo variável por unidade. Na física, a função afim é aplicada para descrever movimentos retilíneos uniformes, onde a posição de um objeto em movimento pode ser representada em função do tempo.
Vejamos exemplos concretos:
- Economia: Um exemplo clássico é a análise de custo, onde f (x) = ax + b representa o custo total f (x), sendo a o custo variável por unidade produzida e b o custo fixo (como aluguer e impostos). Por exemplo, numa fábrica, b pode representar o custo de manutenção das máquinas, enquanto a é o custo de produção unitária;
- Física: em cinemática, a função afim é usada para descrever movimentos retilíneos uniformes. Neste caso, a representa a velocidade constante de um objeto em movimento, e b é a posição inicial. Desta forma, a posição y do objeto em relação ao tempo x é dada por uma função afim, permitindo prever a posição futura do objeto;
- Engenharia e estatística: na engenharia, as funções afins ajudam a descrever relações simples entre variáveis de projeto. Na estatística, são utilizadas em modelos de regressão linear, onde se ajusta uma linha reta a um conjunto de dados para investigar a relação entre variáveis, por exemplo, para estimar como uma alteração numa variável impacta outra;
- Administração e finanças: as funções afins ajudam a calcular receitas e lucros. Suponha uma empresa que vende um produto por um preço fixo: a receita total f (x) é dada pela função f (x) = px, onde p é o preço por unidade e x o número de unidades vendidas. Em modelos de precificação e controlo financeiro, esta relação linear permite otimizar lucros e custos;
- Outras Ciências: em biologia e química, as funções afins aparecem na descrição de certos processos biológicos, como crescimento celular ou reações de primeira ordem em cinética química.
No fundo, a função afim é um dos conceitos fundamentais na matemática, porque permite a compreensão e a representação gráfica de relações lineares.
A sua compreensão é essencial para o estudo de funções mais avançadas e para a aplicação da matemática em problemas práticos, principalmente porque as funções lineares aparecem frequentemente em diversas áreas do conhecimento.
Ao dominar as funções afins, os alunos estão preparados para lidar com uma ampla variedade de problemas matemáticos e científicos, com uma ferramenta poderosa para modelar e entender o mundo ao seu redor. E se precisar de ajuda, os professores de matemática da Superprof estão disponíveis para lhe ensinar a fórmula da função afim!
Resumir com IA